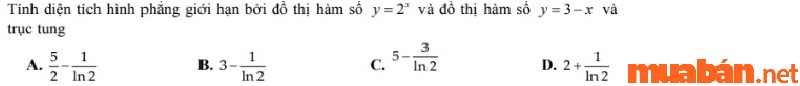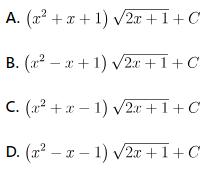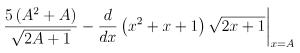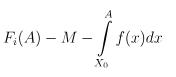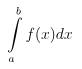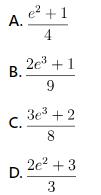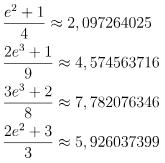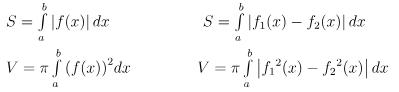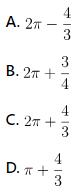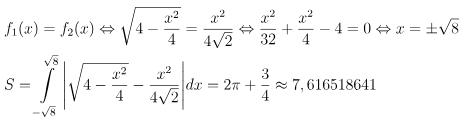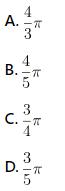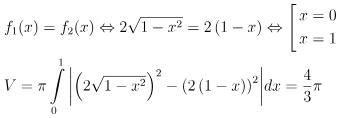Trong lĩnh vực tính toán và xử lý dữ liệu, nguyên hàm là một khái niệm toán học được sử dụng rộng rãi. Khi tính nguyên hàm, sử dụng máy tính sẽ giúp chúng ta tính toán nhanh chóng và chính xác hơn. Trong bài viết này, chúng ta sẽ khám phá cách bấm máy tính nguyên hàm một cách hiệu quả. Hãy cùng với Mua Bán khám phá chi tiết trong bài viết này.

1. Tóm tắt kiến thức về nguyên hàm
1.1 Khái niệm
Nguyên hàm là khái niệm trong giải tích tích phân, được sử dụng để tìm hàm số gốc mà khi đạo hàm sẽ cho ra một hàm số đã biết trước. Khái niệm này được áp dụng rộng rãi trong tính toán, vật lý, và các lĩnh vực khác.
Cho hàm số y = f(x) xác định trên tập A. Hàm F(x) lúc này được gọi là nguyên hàm của f(x) trên A nếu đạo hàm của F(x) là F'(x) = f(x) với mọi x ∊ A
A là khoảng, nữa khoảng, đoạn hoặc nửa đoạn trên R
Họ tất cả các nguyên hàm của hàm số f(x) ký hiệu là ∫f(x) = F(x)+ C .
Chú ý: Mọi hàm số liên tục trên A đều có nguyên hàm trên A.
Xem thêm: Chi Tiết Cách Bấm Máy Tính Chỉnh Hợp Kèm Ví Dụ Minh Hoạ
1.2 Định lý
Định lý cơ bản về nguyên hàm là một định lý quan trọng trong tích phân, có tổng cộng 3 định lý của nguyên hàm là:
- Định lý 1:
Khi F(x) là một nguyên hàm của hàm số f(x) trên khoảng K, thì bất kỳ hàm số G(x) = F(x) + C nào ở mọi hằng số C cũng sẽ là một nguyên hàm của f(x) trên K.
- Định lý 2:
Nếu trên khoảng K, F(x) là một nguyên hàm của hàm số f(x), thì tất cả các nguyên hàm của f(x) trên K có thể được biểu diễn dưới dạng F(x) + C, trong đó C là một hằng số bất kỳ.
- Định lý 3: Tất cả hàm số f(x) liên tục đều có nguyên hàm trên K
3. Công thức
Trước khi tìm hiểu cách bấm máy tính nguyên hàm, ta cần ghi các công thức nguyên hàm để áp dụng vào tính toán. Có 4 bảng công thức nguyên hàm như sau:
- Bảng công thức nguyên hàm cơ bản

- Bảng công thức nguyên hàm mở rộng

- Bảng công thức nguyên hàm nâng cao
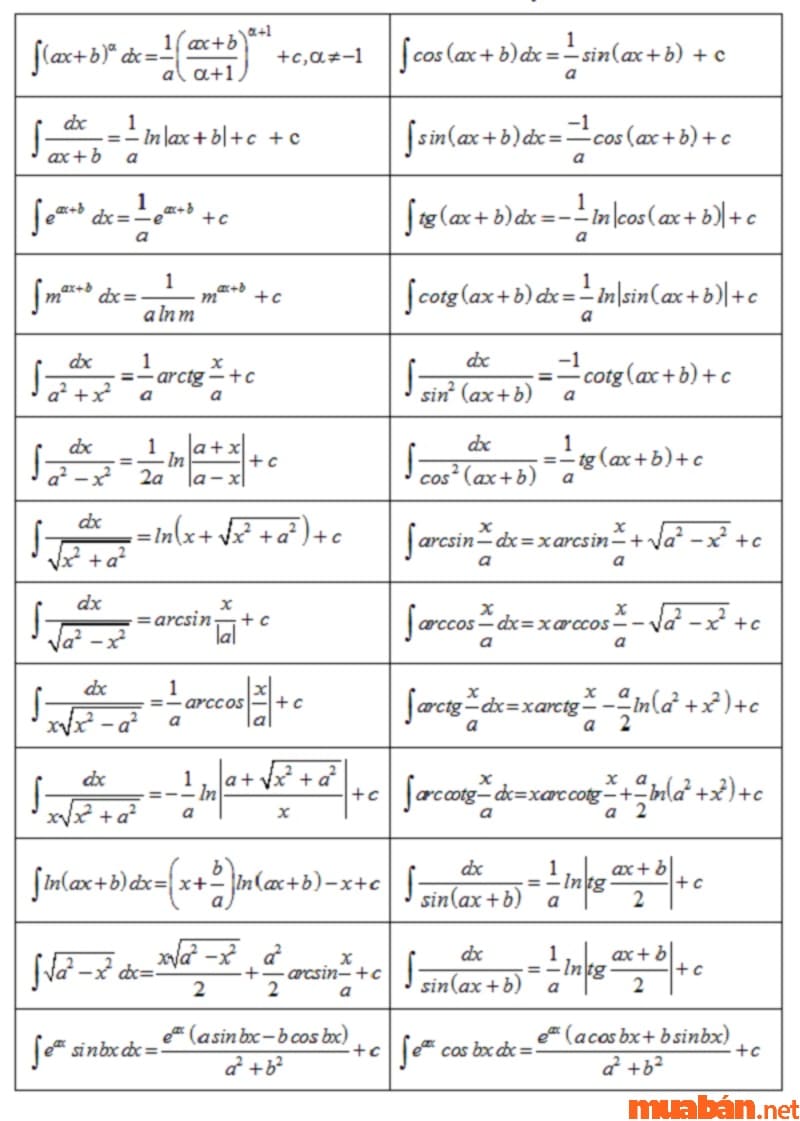
- Bảng nguyên hàm hàm số lượng giác

4. Các tính chất
Có 4 tính chất của nguyên hàm cần bạn đọc ghi nhớ khi tìm hiểu cách bấm máy tính nguyên hàm, cụ thể như sau:
- Trường hợp f(x) là hàm số có nguyên hàm thì (∫f(x)dx)’ = f(x) và ∫f′(x)dx = f(x) + C
- Trường hợp F(x) có đạo hàm là ∫d(F(x)) = F(x) + C
- Tích của nguyên hàm với k là hằng số khác 0 là ∫kf(x)dx = k*∫f(x)dx.
- Tổng và hiệu của nguyên hàm là ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx
| Ngoài ra, bạn có thể tham khảo các tin đăng về việc làm tại website Muaban.net dưới đây: |
Xem thêm: Hướng dẫn chi tiết cách tính hàm Sum trong Excel hiệu quả
2. Cách bấm máy tính nguyên hàm
2.1 Tìm nguyên hàm F(x) của hàm số f(x)

Thay một số x bất kỳ (nằm trong khoảng mà đề đã cho nếu có) trừ cho đạo hàm đáp án đề cho.
- Nếu kết quả nguyên hàm cho ít nhất một giá trị khác 0, ta loại bỏ phương án đó.
- Nếu kết quả nguyên hàm luôn bằng 0 với một dãy giá trị A, ta chọn phương án đó.

- Video cách bấm máy tính nguyên hàm: Tìm nguyên hàm F(x) của hàm số f(x)
2.2 Tìm 1 nguyên hàm F(x) của hàm số f(x) biết F(x0) = M

Thay một số A bất kỳ vào đề, lấy đề trừ cho nguyên hàm chạy từ x đề cho đến số đã gán
- Nếu kết quả cho ít nhất một giá trị khác 0, ta loại bỏ phương án đó.
- Nếu kết quả luôn bằng 0 với một dãy giá trị A, ta chọn phương án đó.

- Video cách bấm máy tính nguyên hàm: Tìm 1 nguyên hàm F(x) của hàm số f(x) biết F(x0) = M
2.3 Tính tích phân
Để bấm dấu tích phân trên máy tính, bạn làm như sau:
- Nhấn vào biểu tượng tích phân (thường nằm dưới nút ALPHA hoặc có biểu tượng “∫”).
- Nhập phương trình vào ô giữa để xác định hàm mà bạn muốn tích phân.
- Nhập giá trị cận trên vào ô vuông nhỏ phía trên phương trình.
- Nhập giá trị cận dưới vào ô vuông nhỏ phía dưới phương trình.

Để kiểm tra đáp án nào cho kết quả là số lẻ giống với kết quả tích phân bấm trên máy tính, làm như sau:
- Bấm đề và nhập phương trình vào máy tính.
- Lần lượt bấm vào 4 đáp án để xem kết quả tích phân của từng đáp án.
- Kiểm tra từng đáp án xem có kết quả tích phân là số lẻ giống với kết quả bấm trên máy tính không.
- Chọn đáp án mà kết quả tích phân là số lẻ giống với kết quả bấm trên máy tính.

- Video cách bấm máy tính nguyên hàm: Tính tích phân
2.4 Diện tích hình phẳng – Thể tích khối tròn xoay
Cách bấm máy tính nguyên hàm khi tính diện tích hình phẳng và thể tích khối tròn xoay như sau:
- Nhập công thức tính vào máy để cho ra kết quả
- Lần lượt nhập các đáp án để kiểm tra kết quả của từng đáp án.
- Kiểm tra từng đáp án có giống với kết quả máy tính cho ra không.
- Chọn đáp án giống kết quả trên máy tính.
- Ví dụ bài Diện tích hình phẳng
Hướng dẫn bấm máy
Bước 1: Nhập vào máy tính
Bước 2: Nhập đáp án đề cho >>> Nhấn = để kiểm tra các đáp án có giống với kết quả đã bấm máy
>>> Đáp án: A
- Ví dụ bài Thể tích khối tròn xoay
Hướng dẫn bấm máy
Bước 1: Nhập vào máy tính biểu thức
Bước 2: Nhập đáp án đề cho >>> Nhấn = để kiểm tra các đáp án có giống với kết quả đã bấm máy
>>> Đáp án: C
- Video cách bấm máy tính nguyên hàm: Diện tích hình phẳng – Thể tích khối tròn xoay
3. Các bài giải hệ phương trình thường gặp
Bên cạnh việc biết cách bấm máy tính nguyên hàm, Mua Bán cũng xin chia sẻ các bài giải hệ phương trình thường gặp. Có 4 dạng bài giải bao gồm:
- Dạng 1: Tìm nguyên hàm F(x) của hàm số f(x)
Trong đó:
f(A): là giá trị của hàm f(x) tại x = A, với A là một hằng số bất kỳ thuộc vào tập xác định. Các giá trị A có thể lấy là 0.1, 0.2, 0.3, …, 1, 1.1.
Fi(x): là các kết quả của phép tích phân nguyên hàm của hàm f(x).
Câu hỏi bài tập: 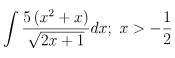
Hướng dẫn giải bài:
Bước 1: Nhập
Bước 2:
Gán x = A = 1 hoặc 0.1 (bấm CALC → A) để kiểm tra kết quả khác 0. Nếu kết quả khác 0, loại bỏ ngay đáp án đó. >>> Loại trừ phương án A.
Thay Fi(x) bằng đáp án B và gán A như trên để kiểm tra kết quả. Nếu kết quả khác 0, loại bỏ đáp án đó. >>> Loại trừ phương án B.
Thay Fi(x) bằng đáp án C và gán A như trên để kiểm tra kết quả. Nếu kết quả bằng 0, kiểm tra thêm một số giá trị khác của A như 0, 0.2, 0.5, 1. Nếu kết quả vẫn là 0, chọn phương án C. (Lưu ý: Không nên gán x = A với giá trị quá lớn vì máy tính có thể không xử lý được).
>>> Đáp án: C
- Dạng 2: Tìm 1 nguyên hàm F(x) của hàm số f(x) biết F(x0) = M
Cú pháp:
Câu hỏi bài tập: Tìm nguyên hàm F(x) của hàm số
Hướng dẫn giải bài
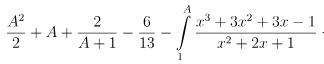
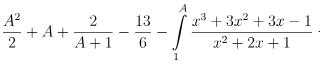
>>> Đáp án: D
Xem thêm: Hướng dẫn cách đánh dấu chấm trong Word nhanh chóng và đơn giản
- Dạng 3: Tính tích phân:
Cú pháp:
Câu hỏi bài tập: 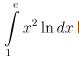
Hướng dẫn giải bài
>>> Đáp án: B
- Dạng 4: Diện tích hình phẳng – Thể tích khối tròn xoay
Cú pháp:
Câu hỏi bài tập 1: Tính diện tích hình phẳng giới hạn bởi các đường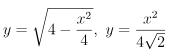
Hướng dẫn giải bài tập 1
Phương trình hoành độ giao điểm:
>>> Đáp án: C
Câu hỏi bài tập 2: Tính thể tích của khối tròn xoay khi (H) giới hạn bởi các đường và y = 2(1 – x) xoay quanh trục Ox.
Hướng dẫn giải bài tập 2
Phương trình hoành độ giao điểm:
>>> Đáp án: A
4. Các lưu ý khi giải các bài nguyên hàm
Khi tìm hiểu cách bấm máy tính nguyên hàm để giải các bài toán, cần lưu ý một số điều quan trọng sau đây:
Đọc đề cẩn thận: hãy đọc đề bài cẩn thận để hiểu rõ yêu cầu và điều kiện của bài toán. Điều này sẽ giúp bạn xác định đúng hàm mà bạn đang cần tích phân.
Kiểm tra tập xác định: Xác định tập xác định của hàm mà bạn đang tính nguyên hàm để đảm bảo các giá trị của biến độc lập nằm trong tập xác định này.
Sử dụng đúng công thức: Sử dụng các đúng các công thức tính nguyên hàm như hàm mũ, hàm logarit, hàm lượng giác, v.v.

Kiểm tra kỹ thuật tính toán: Hãy đảm bảo rằng bạn đã áp dụng đúng các kỹ thuật tính toán, như phân tích thành tổng, phân rã hàm thành các thành phần đơn giản hơn, hoặc sử dụng các phép biến đổi để đưa về dạng phù hợp cho tích phân.
Kiểm tra đáp án cuối cùng: Sau khi tính toán xong, hãy kiểm tra lại kết quả và đảm bảo nó đúng với yêu cầu của bài toán.
Lưu ý về hằng số: Khi tính nguyên hàm, lưu ý hằng số (C) xuất hiện trong kết quả không xác định và bạn có thể thêm hoặc loại bỏ nó tùy thuộc vào yêu cầu của bài toán.
Lời kết
Trong bài viết này, chúng ta đã tìm hiểu về cách bấm máy tính nguyên hàm một cách hiệu quả. Việc sử dụng máy tính giúp chúng ta tiết kiệm thời gian và đảm bảo tính chính xác trong quá trình tính toán. Hy vọng chia sẻ trên sẽ giúp bạn áp dụng tính toán nguyên hàm trong các bài toán phức tạp một cách dễ dàng. Ngoài ra, đừng quên bỏ qua những bài viết khác ở mục chia sẻ kinh nghiệm, tìm việc làm tại Muaban.net
Xem thêm
- Hướng dẫn cách in 2 mặt trong Word chi tiết, nhanh chóng
- Cách in Excel vừa trang giấy A4 cực đơn giản, nhanh chóng
- Cách bấm log trên máy tính fx 580VN cho các dạng toán
- 7 app giải bài tập nguyên lý thống kê được tải nhiều nhất